Understanding the Invariancy of Space-Time Interval Equations with Mathematical Proof!!!
In the last article, I explained about Lorentz Transformation in a very simple way and in this article, we are going use that beast.
In this article, I going to explain the invariancy of Spacetime
interval equations in a mathematical way.
But before you continue, you have to read my articles on Introduction to Space-Time and Lorentz Transformation to understand this article in a better
way.
Let’s get started….
As I have explained in my article on Introduction to Space-time, as it
sounds, made up of two critical words, space and time. Space, as per the
traditional physics, represents the 3-dimensional coordinate system of our
universe. Scientists before Einstein believed that our universe is limited to
these 3 coordinates (x, y and z-axis) and the universe according to this
convention is called Newtonian. But, in 1905, Einstein showed in his Special
Theory of relativity that time is also an integral factor. Well, it was not
before 1908, when one of the Einstein’s own professor and renowned physicist
Herman Minkowski proposed the concept of the union of space and time as a way to
reformulate Special Relativity and by this way, the concept of space-time was
born.
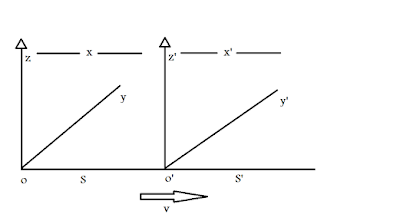
To derive the equations to prove its invariancy, we need to understand
the above picture. Here in this picture, there are two coordinate systems, S
and S’. Space and time coordinate of S are x, y, z and t, and for S’ they
are x’, y’, z’ and t’.
Now, suppose, in the course of motion of S’ relative to S in the
x-direction with a speed v, a flash of light is emitted at the origins of S and
S’ when they were just coincident. Let’s identify that instant as t=0=t’.
Using this picture, I derived the Lorentz transformation equations in
my Introduction to Lorentz Transformation article and in this article, we are going
to find the space-time interval equation using it.
Proof of Invariancy
As we all know,
Time = Distance / Velocity
t = √ (x² + y² + z²) / c
c² t² = x² + y² + z² (1)
Distance = √ (x² + y² + z²), because it has 3 axes.
Now, to prove invariancy, we need to show,
x² + y² + z² – c² t² = x’² + y’²+ z’² – c² t’² (2)
Why??? Because invariancy means in every condition, the space-time
interval equation in both S and S’ will be equal. Which means that we can write
the space-time interval equation for S and S’ plane and equate them as we did
in equation 2.
Now, proving LHS = RHS,
Where, LHS = x² + y² + z² – c² t² (space-time interval equation in S plane)
And, RHS = x’² + y’² + z’² – c² t’²
Now, using Lorentz Transformations in RHS,
[x – vt / (√ 1 – v²/c²)]² + y² + z² – c² [(t – vx/c²) / (√ 1 – v²/c²)]² (3)
Since,
x’ = x – vt / (√ 1 – v²/c²)
y’ = y
z’ = z
t’ = (t – vx/c²) / (√ 1 – v²/c²)
Now if you solve equation 3, you will get,
x² + y² + z² – c² t²
which is our LHS.
Thus, LHS = RHS and invariancy of the space-time interval is proved.
Same can also be proved by inverse Lorentz Transforms and putting
those in LHS and then deriving RHS from it. The choice is yours always!!!
So, that’s its guys…that’s all about Space-time intervals and its
invariancy.
In my upcoming articles, I will write about 4-vectors, tensors etc. are very important to understand
relativity and cosmology in general. So, I will be writing about these gems,
very soon…
Once these articles will be available links will be provided here...
-Ratnadeep Das Choudhury













0 Comments