Lorentz Transformation: A Simplified Overview

Okay…. there are already a lot of articles and books have been written on this topic, but still, I need to cover this for two main reasons. First, my upcoming articles will be based on this topic and I don’t want my readers to have trouble while finding adequate material to understand this topic. Second, as I have also studied many articles and books about this topic, so while reading them I always felt that there is always the ‘student’s side’ of the explanation was missing from the text. So, in this article I will try to include that.

Lorentz transform plays a critical and fundamental role in the space of relativity. Without it you cannot derive the expressions for the popular theories like length contraction, time-dilation and popular equation of mass-energy relation, e = mc^2. So, by this I hope you can understand the gravity this topic holds.

The Lorentz transformations are named after the Dutch physicist Hendrick Lorentz.

Before, we start the derivation of the transformation, we need to keep two postulates in our memory:

1) These transformations will follow the principle of relativity. The principle of relativity states that, all laws of classical mechanics are valid in any two coordinate systems moving uniformly relative to each other

2) The universal constancy of the speed of light in vacuum will not be violated

So, now you are ready to jump into the juicy derivation part….

Derivation of Lorentz transformations

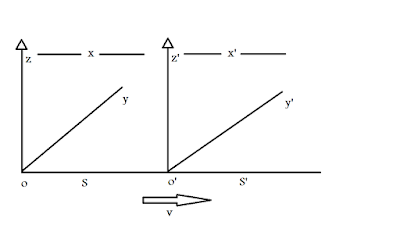
Suppose, there are two co-ordinate systems, S and S’. The space and time coordinate of S are x, y, z and t, and for S’ they are x’, y’, z’ and t’.

Now, suppose, in the course of motion of S’ relative to S in the x-direction with a speed v, a flash of light is emitted at the origins of S and S’ when they were just coincident. Let’s identify that instant as t=0=t’.

So, for each observer, the flash of light would spread out like a spherical wave with speed c according to two postulates, so for each wave,

Time = Distance / speed

t = √ (x² + y² + z²) / c

c² t² = x² + y² + z²    (1)

Distance = √ (x² + y² + z²), because it has 3 axes.

Equation 1 is called a Spacetime interval equation.

Now, as the spacetime interval is invariant, we can write,

x² + y² + z²- c² t² = x’² + y’² + z’²– c² t’² = 0   (2)

I will write another article to prove equation 2, so, stay tuned for that…

Since the relative motion occurs in the x-direction, the y and z coordinates should remain unchanged,

y = y’

z = z’

Now, after substituting this in equation 2, we get,

x² - c² t² = x’² – c²t’²   (3)

Now, from the figure, at O’, x’ should be 0 but x is vt and at O, x is 0 but x’ is -vt. So, we can write,

x’ = k (x – vt)   (4)

x = k’ (x’ – vt’)   (5)

where, k and k’ are the constants and added for precise measurement.

From eq. (4) and (5), we eliminate x’,

t’ = k [ t – (x/v)(1–1/kk’)]      (6)

Now, from eq. (3), (4) and (6),

x²- c² t² ≡ (k²)(x² – 2xvt + v² t²) – c² k² [t² – (2xt/v)(1 – 1/kk’) + (x²/v²)(1 – 1/kk’)²]  = 0       (7)

By equation the coefficients of t^2, as eq. (7) is an identity and true values for all values of x and t, we get,

– c² = k² v² – k² c²      

k = 1 / √ (1 – v² / c² )      (8)

and this equation is known as Lorentz Factor

and by equating coefficient of xt,

0 = –2k²v + 2(c² k² / v) (1 – 1/k k’)      (9)

Now, using Eq. 8 and 9 in Eq.  4 and 6, we get ,

x’ = x – vt / (√ 1 – v²/c²)        (10)

y’ = y       (11)

z’ = z       (12)

t’ = (t – vx/c²) / (√ 1 – v²/c²)    (13)

Eq. 10, 11, 12 and 13 are known as Lorentz transformation or Einstein – Lorentz Transformation.

Also, we can obtain the reverse transformation if we replace x’ with x and t’ with t,

x = x’ – vt’ / (√ 1 – v²/c²)       

y = y’      

z = z’       

t = (t’ – vx’/c²) / (√ 1 – v²/c²)    

Now from Lorentz and its reverse transforms, if v << c then we can ignore the fraction involving v and c as its value will be much lower than one and subtracting it from 1 will give a result which will be approximately equal to 1 and thus we can also obtain the following equations which are also known as Galilean transformation,

x’ = x – vt

y’ = y

z’ = z

t’ = t

It’s interesting, isn’t ???

In my upcoming articles, I will write about spacetime interval and how its invariant, 4-vectors, tensors etc. are very important to understand relativity and cosmology. So, I will be writing about these gems, very soon…

Once these articles will be available links will be provided here...

If you like my articles then please consider subscribing our newsletter and follow this blog to get the latest updates directly to you (buttons are available in the right sidebar if you are viewing in desktop and if you are viewing from mobile then its in the bottom of the page).

To know basics of quantum world, astronomy and space exploration you can check out my book "Through the wormhole" on amazon kindle.

Thanks for Reading!!!

Check out my other blog posts!!!

Don't forget to share this post in your social media handles to enrich everyone's knowledge!!!

To know my other works visit my site - ratnadeepdchoudhury.com

You can directly talk with me on Instagram

To meet more physics Enthusiasts please join our Facebook Page 

Also for the latest updates of my posts join me on Twitter

I also have a youtube channel where I make videos on Productivity & Growth, Physics and Technology. Check it now on YouTube

See you Again!!!!!

                                                                 -Ratnadeep Das Choudhury

                                                  Founder and writer of The Dynamic Frequency